(4) Sliding window & Optimization 파트 중요 코드 정리
1. Optimizing local parameters
1) void Estimator::vector2double()
for (int i = 0; i <= WINDOW_SIZE; i++)
{
para_Pose[i][0] = Ps[i].x();
para_Pose[i][1] = Ps[i].y();
para_Pose[i][2] = Ps[i].z();
Quaterniond q{Rs[i]};
para_Pose[i][3] = q.x();
para_Pose[i][4] = q.y();
para_Pose[i][5] = q.z();
para_Pose[i][6] = q.w();
if(USE_IMU)
{
para_SpeedBias[i][0] = Vs[i].x();
para_SpeedBias[i][1] = Vs[i].y();
para_SpeedBias[i][2] = Vs[i].z();
para_SpeedBias[i][3] = Bas[i].x();
para_SpeedBias[i][4] = Bas[i].y();
para_SpeedBias[i][5] = Bas[i].z();
para_SpeedBias[i][6] = Bgs[i].x();
para_SpeedBias[i][7] = Bgs[i].y();
para_SpeedBias[i][8] = Bgs[i].z();
}
}
for (int i = 0; i < NUM_OF_CAM; i++)
{
para_Ex_Pose[i][0] = tic[i].x();
para_Ex_Pose[i][1] = tic[i].y();
para_Ex_Pose[i][2] = tic[i].z();
Quaterniond q{ric[i]};
para_Ex_Pose[i][3] = q.x();
para_Ex_Pose[i][4] = q.y();
para_Ex_Pose[i][5] = q.z();
para_Ex_Pose[i][6] = q.w();
}
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < f_manager.getFeatureCount(); i++)
para_Feature[i][0] = dep(i);
para_Td[0][0] = td;
- para_Pose[i][]에는 WINDOW내 i번째 frame에서의 Ps(\(p_{b_k}^{w}\)), Rs(\(q_{b_k}^{w}\))를 넣어준다. para_SpeedBias에는 Vs(\(v_{b_k}^{w}\)), Bas(\(b_a^w\)), Bgs(\(b_g^w\))를 넣어준다. 또한 para_Ex_Pose에는 tic (\(p_c^b\)), ric (\(q_c^b)\)값을 넣어준다. para_Feature에는 각 feature의 inverse depth를 넣어준다. (Because of numerical stability : (\(d_{min}\), ∞) → (0, 1/ \(d_{min}\)) )
- void Estimator::optimization()
loss_function = new ceres::HuberLoss(1.0);
for (int i = 0; i < frame_count + 1; i++)
{
ceres::LocalParameterization *local_parameterization = new PoseLocalParameterization();
problem.AddParameterBlock(para_Pose[i], SIZE_POSE, local_parameterization);
if(USE_IMU)
problem.AddParameterBlock(para_SpeedBias[i], SIZE_SPEEDBIAS);
}
if(!USE_IMU)
problem.SetParameterBlockConstant(para_Pose[0]);
for (int i = 0; i < NUM_OF_CAM; i++)
{
ceres::LocalParameterization *local_parameterization = new PoseLocalParameterization();
problem.AddParameterBlock(para_Ex_Pose[i], SIZE_POSE, local_parameterization);
if ((ESTIMATE_EXTRINSIC && frame_count == WINDOW_SIZE && Vs[0].norm() > 0.2) || openExEstimation)
openExEstimation = 1;
else
problem.SetParameterBlockConstant(para_Ex_Pose[i]);
}
problem.AddParameterBlock(para_Td[0], 1);
if (!ESTIMATE_TD || Vs[0].norm() < 0.2)
problem.SetParameterBlockConstant(para_Td[0]);
...
if(USE_IMU)
{
for (int i = 0; i < frame_count; i++)
{
int j = i + 1;
if (pre_integrations[j]->sum_dt > 10.0)
continue;
IMUFactor* imu_factor = new IMUFactor(pre_integrations[j]);
problem.AddResidualBlock(imu_factor, NULL, para_Pose[i], para_SpeedBias[i], para_Pose[j], para_SpeedBias[j]);
}
}
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (it_per_id.used_num < 4)
continue;
++feature_index;
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;
Vector3d pts_i = it_per_id.feature_per_frame[0].point;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
if (imu_i != imu_j)
{
Vector3d pts_j = it_per_frame.point;
ProjectionTwoFrameOneCamFactor *f_td = new ProjectionTwoFrameOneCamFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td);
problem.AddResidualBlock(f_td, loss_function, para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0]);
}
f_m_cnt++;
}
}
...
ceres::Solve(options, &problem, &summary);
...
-
para_Pose, para_SpeedBias를 고정 변수로 지정하고 para_Pose[0]은 reference값으로 고정시킨다. 또한 한번이라도 Vs > 0.2값을 발견하면 지속적으로 parameter로 지정한다.
여기서 LocalParameterization은 quaternion의 over-parametrization을 줄이기 위해 so(3)로 바꿔 계산하는 것으로, manifold상에서 계산 후 다시 쿼터니언의 increment로 돌리는 작업도 수행된다.
[ref] : http://ceres-solver.org/nnls_modeling.html#localparameterization
- frame의 pre_integration이 10초 이하로 지난 것만 imu_factor를 이용하여 parameter로 추가한다. 이때 i번째 frame과 그 다음 frame의 para_Pose, para_SpeedBias를 추가해준다.
그런데, IMUFactor의 경우 다른 Factor들과 다르게 WINDOW_SIZE - 1개를 parameter로 넣어준다. 이는 IMU의 measurement model이 i와 i+1사이의 delta를 가지고 residual을 구하기 때문이다.
- frame의 pre_integration이 10초 이하로 지난 것만 imu_factor를 이용하여 parameter로 추가한다. 이때 i번째 frame과 그 다음 frame의 para_Pose, para_SpeedBias를 추가해준다.
- td는 time offset으로, 최적화가 필요하면 parameter로 지정하지만, 필요없다고 초기에 설정되면 고정한다. (참고 : image time + td = IMU time)
- marginalization관련 내용은 chapter5에서 다룰 예정.
-
모든 feature에 대해 for문을 돌면서 Huber loss function과 함께 ProjectionTwoFrameOneCamFactor을 cost function으로 추가한다. 이때 parameter는 para_Pose와 para_Ex_Pose[0], para_Feature (inverse depth), para_Td[0]이다.
- double2vector를 통해 optimize된 값을 다시 Ps, Rs, Vs, Bas, Bgs, tic, ric, f_manager의 depth값들에 넣어준다.
-
Ceres Solver의 state estimation에 대한 설명 :
\(P(x | z)\) : posterior probability, \(P(x)\) : priori probability, \(P(z|x)\) likelihood probability일때 다음식을 계산하는 것이다.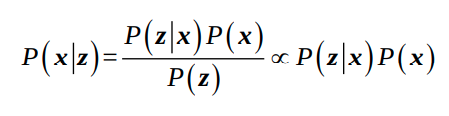
Posterior probability를 계산하는 것은 어렵지만, maximize하는 state를 찾는것은 상대적으로 쉽다.
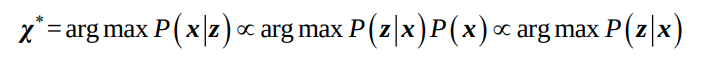
가우시안을 가정하면, 다음과 같이 minimize해야하는 것을 알 수 있다.
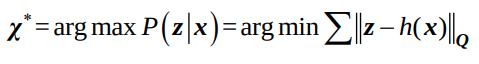
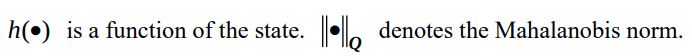
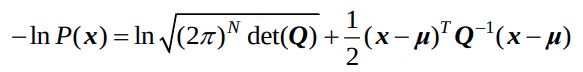
-
이제, VINS-Mono (Fusion)의 cost function인 다음을
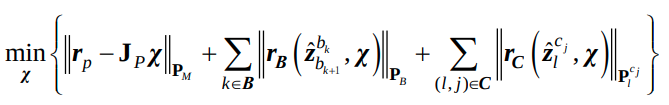
(이때 \((r_p, J_p)\)는 prior information from marginalization, \(r_B\)는 IMU의 residual, B는 sliding window 내의 IMU measurements, \(r_C\)는 residual of visual model, C는 set of features observed at least two times in sliding windows를 나타낸다.)
최소화 하는 state는 다음과 같이 생각해 볼 수 있다.
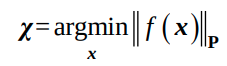
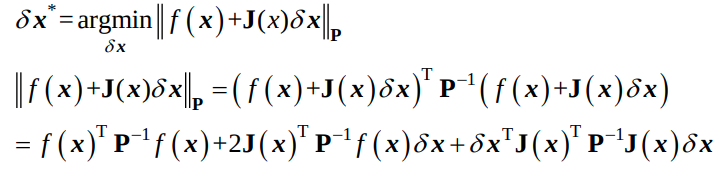
Taylor expansion을 통해 initial에서 delta x를 찾는 것으로 문제를 전환할 수 있고,
SVD를 통해서 다음식을 푸는 것으로 귀결된다.
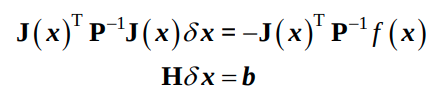
따라서 ceres::Solve를 하게되면, 각 cost function의 evaluate를 통해 jacobian과 residual을 계산하게 되고, 이를통해 non-linear optimization을 parameter들을 조정하게 된다.
3) void Estimator::double2vector()
Vector3d origin_R0 = Utility::R2ypr(Rs[0]);
Vector3d origin_P0 = Ps[0];
if (failure_occur)
{
origin_R0 = Utility::R2ypr(last_R0);
origin_P0 = last_P0;
failure_occur = 0;
}
if(USE_IMU)
{
Vector3d origin_R00 = Utility::R2ypr(Quaterniond(para_Pose[0][6],
para_Pose[0][3],
para_Pose[0][4],
para_Pose[0][5]).toRotationMatrix());
double y_diff = origin_R0.x() - origin_R00.x();
//TODO
Matrix3d rot_diff = Utility::ypr2R(Vector3d(y_diff, 0, 0));
if (abs(abs(origin_R0.y()) - 90) < 1.0 || abs(abs(origin_R00.y()) - 90) < 1.0)
{
ROS_DEBUG("euler singular point!");
rot_diff = Rs[0] * Quaterniond(para_Pose[0][6],
para_Pose[0][3],
para_Pose[0][4],
para_Pose[0][5]).toRotationMatrix().transpose();
}
for (int i = 0; i <= WINDOW_SIZE; i++)
{
Rs[i] = rot_diff * Quaterniond(para_Pose[i][6], para_Pose[i][3], para_Pose[i][4], para_Pose[i][5]).normalized().toRotationMatrix();
Ps[i] = rot_diff * Vector3d(para_Pose[i][0] - para_Pose[0][0],
para_Pose[i][1] - para_Pose[0][1],
para_Pose[i][2] - para_Pose[0][2]) + origin_P0;
Vs[i] = rot_diff * Vector3d(para_SpeedBias[i][0],
para_SpeedBias[i][1],
para_SpeedBias[i][2]);
Bas[i] = Vector3d(para_SpeedBias[i][3],
para_SpeedBias[i][4],
para_SpeedBias[i][5]);
Bgs[i] = Vector3d(para_SpeedBias[i][6],
para_SpeedBias[i][7],
para_SpeedBias[i][8]);
}
}
else
{
for (int i = 0; i <= WINDOW_SIZE; i++)
{
Rs[i] = Quaterniond(para_Pose[i][6], para_Pose[i][3], para_Pose[i][4], para_Pose[i][5]).normalized().toRotationMatrix();
Ps[i] = Vector3d(para_Pose[i][0], para_Pose[i][1], para_Pose[i][2]);
}
}
if(USE_IMU)
{
for (int i = 0; i < NUM_OF_CAM; i++)
{
tic[i] = Vector3d(para_Ex_Pose[i][0],
para_Ex_Pose[i][1],
para_Ex_Pose[i][2]);
ric[i] = Quaterniond(para_Ex_Pose[i][6],
para_Ex_Pose[i][3],
para_Ex_Pose[i][4],
para_Ex_Pose[i][5]).normalized().toRotationMatrix();
}
}
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < f_manager.getFeatureCount(); i++)
dep(i) = para_Feature[i][0];
f_manager.setDepth(dep);
if(USE_IMU)
td = para_Td[0][0];
[논문언급] In contrast, for monocular VINS, thanks to the addition of IMU, drift only occurs in 4 DOF, which is the 3D translation, and the rotation around the gravity direction (yaw angle).
: 즉, IMU를 추가하였으면 rotation drift가 yaw값에서만 발생하는 것이 이론적으로 맞다는 것
-
origin_R0 : \(R_{b_0}^w\), origin_P0 : \(R_{b_0}^w\), origin_R00 : optimized된 \(R_{b_0}^w\),
IMU는 yaw값을 알 수 없으므로, y_diff값은 optimization에서 marginalization, visual measurements로부터 구해진 것이다. 그런데 사실 R0, P0는 이미 이전에 optimization이 진행되었으므로 다시 바뀔 이유가 없는 parameter이나, yaw에서의 drift로 인해 optimization에서 변경될 수 있다. 또한, Initialization에서 이미 Identity로 지정하고 시작하기 때문에, yaw값의 변경은 drift로 생각해 볼수 있다.
따라서, 이 drift를 없애기 위해 rot_diff를 통해 yaw값의 추가값을 삭제한다. (이전 - 현재의 yaw값 이므로)
- yaw각도가 90도 근처라면, gimbal lock에 해당하는 singular point이므로, yaw값이 제대로 구해지지 않을 수 있어 rotation matrix의 차이로 rot_diff를 구한다.
2. Cost function factors
1) virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const, (imu_factor.h)
...
Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);
residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj);
Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();
residual = sqrt_info * residual;
if (jacobians)
{
double sum_dt = pre_integration->sum_dt;
Eigen::Matrix3d dp_dba = pre_integration->jacobian.template block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = pre_integration->jacobian.template block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = pre_integration->jacobian.template block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = pre_integration->jacobian.template block<3, 3>(O_V, O_BG);
if (jacobians[0])
{
Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
jacobian_pose_i.setZero();
jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));
jacobian_pose_i = sqrt_info * jacobian_pose_i;
}
if (jacobians[1])
{
Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_i(jacobians[1]);
jacobian_speedbias_i.setZero();
jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;
jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * pre_integration->delta_q).bottomRightCorner<3, 3>() * dq_dbg;
jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;
jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i = sqrt_info * jacobian_speedbias_i;
}
if (jacobians[2])
{
Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_j(jacobians[2]);
jacobian_pose_j.setZero();
jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_j.block<3, 3>(O_R, O_R) = Utility::Qleft(corrected_delta_q.inverse() * Qi.inverse() * Qj).bottomRightCorner<3, 3>();
jacobian_pose_j = sqrt_info * jacobian_pose_j;
}
if (jacobians[3])
{
Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_j(jacobians[3]);
jacobian_speedbias_j.setZero();
jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();
jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j = sqrt_info * jacobian_speedbias_j;
}
}
- pre_integration의 evaluate를 통해, residual을 구할 수 있다.
- 다음식을 이용하면
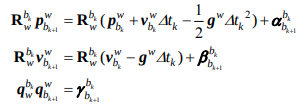
residual은 다음과 같이 표현되며,

코드도 위식과 동일하게 구현된다. 이때 코드상에서 corrected_ prefix가 붙은 \(\hat\gamma^{b_k}_{b_{k+1}}\),\(\hat\alpha^{b_k}_{b_{k+1}}\),\(\hat\beta^{b_k}_{b_{k+1}}\)는 Chapter3에서 본, integrationBase의 jacobian을 통해서 구해진다. (pre_integration)
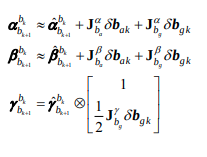
예를 들면, 위의 bias에 대한 approximation을 이용한다. 구해둔 jacobian에서 \(\frac{\delta \hat \alpha^{b_k}_{b_{k+1}}}{\delta b_{a_k}}\)값을 얻어 낼 수 있으므로, \({\delta \hat \alpha^{b_k}_{b_{k+1}}}\) = \(\frac{\delta \hat \alpha^{b_k}_{b_{k+1}}}{\delta b_{a_k}}\) * \({\delta b_{a_k}}\) + \(\frac{\delta \hat \alpha^{b_k}_{b_{k+1}}}{\delta b_{g}}\) * \({\delta b_{g}}\)가 되고, \({\delta b_{a_k}}\) = \(b_{a_k}\) - \(\hat b_{a_k}\), \({\delta b_{g}}\) = \(b_{g}\) - \(\hat b_{g}\)를 이용한다. (bias만이 결국 pre-integration에서 update되지 않았다고 볼 수 있으므로)
즉, new measurement값 \({\hat \alpha^{b_k}_{b_{k+1}}}\) = \({\hat \alpha^{b_k}_{b_{k+1}}}\) + \({\delta \hat \alpha^{b_k}_{b_{k+1}}}\)를 “pre-integration”의 jacobian을 통해 계산한다. 이에 따라 더 정확한 residual을 구할 수 있게된다.
- LocalParameterization을 사용함에 따라 overparameterization을 줄여 rotation의 dimension을 하나 줄이는 과정이 언급되었다. 다음 parameter 순서에 따른 jacobian은
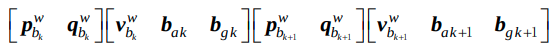
<7,9,7,9> 에서 <6,9,6,9>가 되어야 할 것이다. 즉, J[0]과 J[2]의 마지막 row는 0이된다.
이후 jacobian을 구하는 식은 Formula_Derivation_and_Analysis_of_the_VINS-Mono.pdf에 자세히 설명되어 있으며, 이 문서의 Appendix B에서 Lie algebra를 통한 유도과정까지 알 수 있다. 코드는 동일하게 작성되어 있다. (sqrt_info 변수는 jacobian에 covariance까지 포함하여 계산하기 위함이다.)
2) bool ProjectionTwoFrameOneCamFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const, (projectionTwoFrameOneCamFactor.cpp)
Eigen::Vector3d pts_i_td, pts_j_td;
pts_i_td = pts_i - (td - td_i) * velocity_i;
pts_j_td = pts_j - (td - td_j) * velocity_j;
Eigen::Vector3d pts_camera_i = pts_i_td / inv_dep_i;
Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
Eigen::Vector3d pts_w = Qi * pts_imu_i + Pi;
Eigen::Vector3d pts_imu_j = Qj.inverse() * (pts_w - Pj);
Eigen::Vector3d pts_camera_j = qic.inverse() * (pts_imu_j - tic);
Eigen::Map<Eigen::Vector2d> residual(residuals);
double dep_j = pts_camera_j.z();
residual = (pts_camera_j / dep_j).head<2>() - pts_j_td.head<2>();
residual = sqrt_info * residual;
if (jacobians)
{
Eigen::Matrix3d Ri = Qi.toRotationMatrix();
Eigen::Matrix3d Rj = Qj.toRotationMatrix();
Eigen::Matrix3d ric = qic.toRotationMatrix();
Eigen::Matrix<double, 2, 3> reduce(2, 3);
reduce << 1. / dep_j, 0, -pts_camera_j(0) / (dep_j * dep_j),
0, 1. / dep_j, -pts_camera_j(1) / (dep_j * dep_j);
reduce = sqrt_info * reduce;
if (jacobians[0])
{
Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
Eigen::Matrix<double, 3, 6> jaco_i;
jaco_i.leftCols<3>() = ric.transpose() * Rj.transpose();
jaco_i.rightCols<3>() = ric.transpose() * Rj.transpose() * Ri * -Utility::skewSymmetric(pts_imu_i);
jacobian_pose_i.leftCols<6>() = reduce * jaco_i;
jacobian_pose_i.rightCols<1>().setZero();
}
if (jacobians[1])
{
Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_pose_j(jacobians[1]);
Eigen::Matrix<double, 3, 6> jaco_j;
jaco_j.leftCols<3>() = ric.transpose() * -Rj.transpose();
jaco_j.rightCols<3>() = ric.transpose() * Utility::skewSymmetric(pts_imu_j);
jacobian_pose_j.leftCols<6>() = reduce * jaco_j;
jacobian_pose_j.rightCols<1>().setZero();
}
if (jacobians[2])
{
Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_ex_pose(jacobians[2]);
Eigen::Matrix<double, 3, 6> jaco_ex;
jaco_ex.leftCols<3>() = ric.transpose() * (Rj.transpose() * Ri - Eigen::Matrix3d::Identity());
Eigen::Matrix3d tmp_r = ric.transpose() * Rj.transpose() * Ri * ric;
jaco_ex.rightCols<3>() = -tmp_r * Utility::skewSymmetric(pts_camera_i) + Utility::skewSymmetric(tmp_r * pts_camera_i) +
Utility::skewSymmetric(ric.transpose() * (Rj.transpose() * (Ri * tic + Pi - Pj) - tic));
jacobian_ex_pose.leftCols<6>() = reduce * jaco_ex;
jacobian_ex_pose.rightCols<1>().setZero();
}
if (jacobians[3])
{
Eigen::Map<Eigen::Vector2d> jacobian_feature(jacobians[3]);
jacobian_feature = reduce * ric.transpose() * Rj.transpose() * Ri * ric * pts_i_td * -1.0 / (inv_dep_i * inv_dep_i);
}
if (jacobians[4])
{
Eigen::Map<Eigen::Vector2d> jacobian_td(jacobians[4]);
jacobian_td = reduce * ric.transpose() * Rj.transpose() * Ri * ric * velocity_i / inv_dep_i * -1.0 +
sqrt_info * velocity_j.head(2);
}
}
- 코드상에서 residual은 다음 식을 통해 구해진다.
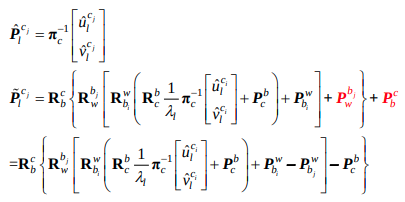
논문과는 달리 tangent basis를 사용하지 않는다. (covariance를 pixel 단위로 계산하고 성능도 더 잘나와서 그렇게 한것으로 추정)
이미 이전에 point들을 normalize해두었기 때문에 \(\pi^{-1}\)은 코드상에 없다.
- 논문에서 언급했듯이, \(\hat u_l^{c_i}, \hat v_l^{c_i}\)는 first observation의 \(l^{th}\) feature이다. 이것을 \(j^{th}\) frame의 feature와 비교하는 것으로, \(\hat u_l^{c_i}, \hat v_l^{c_i}\)를 \(j^{th}\) feature와 matching하여 reprojection error를 비교한다.
또한, td (image time + td = IMU time)와 td_i, td_j는 이론적으로는 같은 값이어야 하지만, optimization parameter에 해당하여 각 frame에서 달라질 수 있다. 즉, IMU와의 보다 정밀한 synchronize를 위해 (td-td_i)*velocity_i 를 빼주게 된다. ()
(optimization에서 td는 IMU pre integration 값을 구하는 것에만 직접적으로 사용되고 pre_integration을 통해 구한 residual과 image에서의 residual이 관련이 있어 synchronize해주는 것으로 보인다.)
이제 \(i^{th}\) frame의 \(l^{th}\) feature를 \(j^{th}\) frame으로 옮긴 \(\tilde P^{c_j}_l\) 를 보면, 논문에서의 수식과 동일한 과정으로 전게 되는 것을 확인할 수 있다.
[논문의 수식 해석]
(1) depth를 곱하여 \(i^{th}\) frame에서의 X,Y,Z 3D points를 구한다. (2) (\(i^{th}\)) IMU frame coordinate로 변환한다. (3) \(i^{th}\) IMU frame에서 world coordinate로 변환한다. (4) world coordinate에서 \(j^{th}\) frame의 IMU coordinate로 변환한다. (5) 최종적으로 \(j^{th}\) frame image coordinate로 변환한다.
- 괄호안으로의 변환은 다음 수식참조, \(P_w^b\) ( b frame 기준 b frame → world origin vector ) + \(R_w^b*P^w_b\) ( b frame기준으로 바꾼 world frame → b frame origin vector) = 0.
qic, tic는 coordinate transform 기준이므로 논문에서의 수식(점변환)을 위해 inverse를 곱한다.
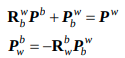
따라서, 3D points를 이미지로 points로 바꾸어 residual은 다음식에 의해 구해진다.
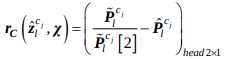
- Jacobian의 경우 chain rule에 의해 다음과 같이 구할 수 있다.
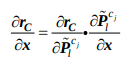
우선 \(\frac{\partial r_c}{\partial \tilde P_l^{c_j}}\)를 먼저 구하면,
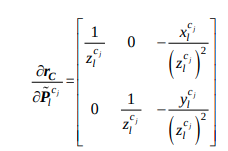
이후, 코드에서 확인할 수 있듯이, \(\frac{\partial \tilde P_l^{c_j}}{\partial \chi}\)를 구할 수 있다. state
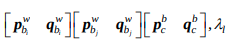
에 대해, 해당 값을 구하고, (Formula_Derivation_and_Analysis_of_the_VINS-Mono.pdf 참조)
최종적으로 위에서 구한 \(\frac{\partial r_c}{\partial \tilde P_l^{c_j}}\) (code의 ‘reduce’)을 곱해주면 Jacobian이 완성된다.
(td에 대한 jacobian은 pdf에 없지만, inverse depth에 대해 구한 것과 유사하며 코드에서 td가 들어가는 부분을 참조하면 쉽게 유도할 수 있다.)
- sqrt_info는 Estimator::setParameter() 에서 다음과 같은 코드
ProjectionTwoFrameOneCamFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity(); 로 지정한 값을 가진다. (information matrix 방식으로 sqrt covariance를 heuristic하게 1.5로 지정한 것으로 보인다.)
3. Sliding Window
initial인 경우, void Estimator::updateLatestStates()를 통해 window에 넣어주지 않은 값들로 fastPredictIMU를 하여 update해주었다. 이후 flag를 initial → non_linear로 바꾸고 window를 sliding 한다.
- fastPredictIMU를 통해서 WINDOW_SIZE+1에 들어온 imu값들을 변수들을 update해준다.
- initial이 아닌경우 sliding window를 먼저하고 이후 updateLatestStates를 하는 이유는, outlier나 failure를 삭제하기 **위함이다. initial의 경우 initialStructure함수에서 충분히 robustness함을 보장해가면서 하기때문에 그런듯 하다.
1) void Estimator::slideWindow()
if (marginalization_flag == MARGIN_OLD)
{
double t_0 = Headers[0];
back_R0 = Rs[0];
back_P0 = Ps[0];
if (frame_count == WINDOW_SIZE)
{
for (int i = 0; i < WINDOW_SIZE; i++)
{
Headers[i] = Headers[i + 1];
Rs[i].swap(Rs[i + 1]);
Ps[i].swap(Ps[i + 1]);
if(USE_IMU)
{
std::swap(pre_integrations[i], pre_integrations[i + 1]);
dt_buf[i].swap(dt_buf[i + 1]);
linear_acceleration_buf[i].swap(linear_acceleration_buf[i + 1]);
angular_velocity_buf[i].swap(angular_velocity_buf[i + 1]);
Vs[i].swap(Vs[i + 1]);
Bas[i].swap(Bas[i + 1]);
Bgs[i].swap(Bgs[i + 1]);
}
}
Headers[WINDOW_SIZE] = Headers[WINDOW_SIZE - 1];
Ps[WINDOW_SIZE] = Ps[WINDOW_SIZE - 1];
Rs[WINDOW_SIZE] = Rs[WINDOW_SIZE - 1];
if(USE_IMU)
{
Vs[WINDOW_SIZE] = Vs[WINDOW_SIZE - 1];
Bas[WINDOW_SIZE] = Bas[WINDOW_SIZE - 1];
Bgs[WINDOW_SIZE] = Bgs[WINDOW_SIZE - 1];
delete pre_integrations[WINDOW_SIZE];
pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};
dt_buf[WINDOW_SIZE].clear();
linear_acceleration_buf[WINDOW_SIZE].clear();
angular_velocity_buf[WINDOW_SIZE].clear();
}
if (true || solver_flag == INITIAL)
{
map<double, ImageFrame>::iterator it_0;
it_0 = all_image_frame.find(t_0);
delete it_0->second.pre_integration;
all_image_frame.erase(all_image_frame.begin(), it_0);
}
slideWindowOld();
}
}
else
{
if (frame_count == WINDOW_SIZE)
{
Headers[frame_count - 1] = Headers[frame_count];
Ps[frame_count - 1] = Ps[frame_count];
Rs[frame_count - 1] = Rs[frame_count];
if(USE_IMU)
{
for (unsigned int i = 0; i < dt_buf[frame_count].size(); i++)
{
double tmp_dt = dt_buf[frame_count][i];
Vector3d tmp_linear_acceleration = linear_acceleration_buf[frame_count][i];
Vector3d tmp_angular_velocity = angular_velocity_buf[frame_count][i];
pre_integrations[frame_count - 1]->push_back(tmp_dt, tmp_linear_acceleration, tmp_angular_velocity);
dt_buf[frame_count - 1].push_back(tmp_dt);
linear_acceleration_buf[frame_count - 1].push_back(tmp_linear_acceleration);
angular_velocity_buf[frame_count - 1].push_back(tmp_angular_velocity);
}
Vs[frame_count - 1] = Vs[frame_count];
Bas[frame_count - 1] = Bas[frame_count];
Bgs[frame_count - 1] = Bgs[frame_count];
delete pre_integrations[WINDOW_SIZE];
pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};
dt_buf[WINDOW_SIZE].clear();
linear_acceleration_buf[WINDOW_SIZE].clear();
angular_velocity_buf[WINDOW_SIZE].clear();
}
slideWindowNew();
}
}
- keyframe인 경우:
- Headers, Ps, Rs, pre_integration, linear_acceleration_buf, angular_velocity_buf, dt_buf, Vs, Bas, Bgs에 대해 i = 0, … WINDOW_SIZE-1 까지는 1 … WINDOW_SIZE의 값을 넣어주고, WINDOW_SIZE에는 i=0의 값들이 있게된다. (swap)
- 이후, WINDOW_SIZE의 Headers, Ps, Rs, Vs, Bas, Bgs는 WINDOW_SIZE - 1과 동일하게 값을 설정한다. (IMU값이 들어올때마다 fastPredictIMU와 비슷하게 처리해주었고 optimization동안에 쌓인 것들에 대해서는 updateLatestStates로 fastPredictIMU를 호출해주었으므로 가능하다. 즉 마지막 i=WINDOW_SIZE에서의 parameter는 계속 변동되고 있는것)
- window의 마지막부분에 대해 pre_integration의 경우 지금 acc_0, gyr_o로 IntegrationBase를 만들어주고, dt_buf, linear_acceleration_buf, angular_buf들 비워준다.
- 이후, all_image_frame에서 sliding전에 기존 0번 frame에 해당하는 것을 지워준다.
- slideWindowOld() 함수에서, initial인경우에는 f_manager.removeBack()으로 들어가서 모든 feature들의 start frame을 한개씩 줄이고, 만약 0번째 start frame에 있던 feature였던 경우 feature_per_frame에서 0번째 frame을 삭제한다. 이로인해 feature의 size=0(즉 frame이 더이상 없으면)이면 feature를 삭제한다.
- keyframe이 아닌 경우:
- WINDOW_SIZE-1에 있는 값들을 지워준다. 즉, 모든 frame_count-1에 있는 Headers, Ps, Rs, Vs등의 변수모음들에 대해 frame_count에 있는 값으로 덮어씌운다.
-
물론 dt_buf, linear_acceleration_buf, angular_velocity_buf 에는 값을 쌓는 느낌으로 추가해준다. 즉, 기존 WINDOW_SIZE-1 frame이 없었던 것처럼 처리한 후, (또한 buf의 경우 기존 WINDOW_SIZE를 WINDOW_SIZE-1에 추가해준 후) WINDOW_SIZE에는 새로운 값들을 넣는다.
이는 Chapter2의 processMeasurements()에서 dt를 계산할때 마지막 dt가 curTime까지인 이유이기도 하다.
-
slideWindowNew() 함수의 경우, f_manager.removeFront(frame_count)함수를 호출하여 마찬가지로 feature의 start_frame이 WINDOW_SIZE 였던 경우 WINDOW_SIZE - 1로 지정하고, 그게 아닌경우 feature의 end_frame == frame_count -1인 곳의 frame을 삭제한다. 이것으로 인해 feature의 featurePerFrame이 없으면 feature를 삭제한다.
(그냥 feature_per_frame.end() -1 을 삭제하는 것과 같다)
4. Outlier Rejection & Failure Detection
1) void Estimator::processImage 마무리 (initial이 아닌경우)
if(!USE_IMU)
f_manager.initFramePoseByPnP(frame_count, Ps, Rs, tic, ric);
f_manager.triangulate(frame_count, Ps, Rs, tic, ric);
optimization();
set<int> removeIndex;
outliersRejection(removeIndex);
f_manager.removeOutlier(removeIndex);
if (! MULTIPLE_THREAD)
{
featureTracker.removeOutliers(removeIndex);
predictPtsInNextFrame();
}
if (failureDetection())
{
ROS_WARN("failure detection!");
failure_occur = 1;
clearState();
setParameter();
ROS_WARN("system reboot!");
return;
}
slideWindow();
f_manager.removeFailures();
// prepare output of VINS
key_poses.clear();
for (int i = 0; i <= WINDOW_SIZE; i++)
key_poses.push_back(Ps[i]);
last_R = Rs[WINDOW_SIZE];
last_P = Ps[WINDOW_SIZE];
last_R0 = Rs[0];
last_P0 = Ps[0];
updateLatestStates();
- IMU를 안쓰면 PnP로 WINDOW_SIZE frame의 변수들을 구한다. (fastPredictIMU가 없으므로) 이후 triangulate하여 (chapter3 참고) feature들의 depth를 구한다.
- outliersRejection을 통해 삭제할 feature id를 받아와 f_manager.removeOutlier에서 해당 feature를 삭제한다.
- multi thread가 아니면 feature Track할때 제거해준다. (prev_pts) 또한 남은 feature들을 track 가능하도록 image data로 바꿔준다. (cur_pts)
- failure detection은 하지않는다. (함수에서 바로 false 반환) 그러나 f_manager.removeFailures()에서 depth가 음수인 것을 삭제한다.
2) void Estimator::outliersRejection(set
int feature_index = -1;
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (it_per_id.used_num < 4)
continue;
feature_index ++;
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;
Vector3d pts_i = it_per_id.feature_per_frame[0].point;
double depth = it_per_id.estimated_depth;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
if (imu_i != imu_j)
{
Vector3d pts_j = it_per_frame.point;
double tmp_error = reprojectionError(Rs[imu_i], Ps[imu_i], ric[0], tic[0],
Rs[imu_j], Ps[imu_j], ric[0], tic[0],
depth, pts_i, pts_j);
err += tmp_error;
errCnt++;
//printf("tmp_error %f\n", FOCAL_LENGTH / 1.5 * tmp_error);
}
}
double ave_err = err / errCnt;
if(ave_err * FOCAL_LENGTH > 3)
removeIndex.insert(it_per_id.feature_id);
}
- reprojectionError함수에서 2. Cost function factors와 동일한 방법을 사용해 error를 구한다.
- Covariance를 1.5로 지정하는 것을 고려해볼때, 2 pixel이상 (2 * 1.5 = 3)보다 error가 크면 해당 feature를 removeIndex에 추가한다.
3) void Estimator::outliersRejection(set
int feature_index = -1;
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (it_per_id.used_num < 4)
continue;
feature_index ++;
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;
Vector3d pts_i = it_per_id.feature_per_frame[0].point;
double depth = it_per_id.estimated_depth;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
if (imu_i != imu_j)
{
Vector3d pts_j = it_per_frame.point;
double tmp_error = reprojectionError(Rs[imu_i], Ps[imu_i], ric[0], tic[0],
Rs[imu_j], Ps[imu_j], ric[0], tic[0],
depth, pts_i, pts_j);
err += tmp_error;
errCnt++;
//printf("tmp_error %f\n", FOCAL_LENGTH / 1.5 * tmp_error);
}
}
double ave_err = err / errCnt;
if(ave_err * FOCAL_LENGTH > 3)
removeIndex.insert(it_per_id.feature_id);
}
- reprojectionError함수에서 2. Cost function factors와 동일한 방법을 사용해 error를 구한다.
- Covariance를 1.5로 지정하는 것을 고려해볼때, 2 pixel이상 (2 * 1.5 = 3)보다 error가 크면 해당 feature를 removeIndex에 추가한다.
VINS-Fusion 코드를 정리한 포스트입니다.
- VINS-Fusion Code Review - (1) Image Processing
- VINS-Fusion Code Review - (2) IMU Processing
- VINS-Fusion Code Review - (3) Initialization
- VINS-Fusion Code Review - (4) Sliding window & Optimization
- VINS-Fusion Code Review - (5) Marginalization
- VINS-Fusion Code Review - (6) Graph optimization
Reference
- [2017] Quaternion kinematics for the error-state Kalman filter.pdf
- [2005] Indirect Kalman Filter for 3D Attitude Estimation.pdf
- Formula Derivation and Analysis of the VINS-Mono.pdf
- Marginalization&Shcurcomplement.pptx
- [TRO2012] Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions.pdf
- VINS-Mono.pdf