(3) Initialization 파트 중요 코드 정리
다음은 Initialization에 대한 VINS-Mono논문 설명이다.
Since the scale is not directly observable from a monocular camera, it is hard to directly fuse these two measurements without good initial values. One may assume a stationary initial condition to start the monocular VINS estimator. However, this assumption is inappropriate as initialization under motion is frequently encountered in real-world applications.
- accelerometer bias는 intialization과정동안 무시된다. (zero bias), Accelerometer bias는 gravity vector와 coupled이기 때문에, 그리고 gravity vector의 크기가 비교적 매우 크기 때문에, initialization phase가 매우짧은 것이 그 이유이다.
1. Initialize the Structure
- void Estimator::processImage(const map<int, vector<pair<int, Eigen::Matrix<double, 7, 1»» &image, const double header)
... ImageFrame imageframe(image, header); imageframe.pre_integration = tmp_pre_integration; all_image_frame.insert(make_pair(header, imageframe)); tmp_pre_integration = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]}; ... if (solver_flag == INITIAL) { if (frame_count == WINDOW_SIZE) { bool result = false; if(ESTIMATE_EXTRINSIC != 2 && (header - initial_timestamp) > 0.1) { result = initialStructure(); initial_timestamp = header; } if(result) { optimization(); updateLatestStates(); solver_flag = NON_LINEAR; slideWindow(); ROS_INFO("Initialization finish!"); } else slideWindow(); } }- keyframe인지 판단한 후, 이전에 계산해둔 pre_integration 값과 함께 all_image_frame에 저장한다.
- frame count가 WINDOW_SIZE가 되기 전까지는 아무것도 하지 않고, WINDOW_SIZE가 되면 initialStructure()함수를 통해 IMU와 visual structure가 align되었는지 판단한다. (안되면 sliding한다.)
- bool Estimator::initialStructure()
vector<SFMFeature> sfm_f; for (auto &it_per_id : f_manager.feature) { int imu_j = it_per_id.start_frame - 1; SFMFeature tmp_feature; tmp_feature.state = false; tmp_feature.id = it_per_id.feature_id; for (auto &it_per_frame : it_per_id.feature_per_frame) { imu_j++; Vector3d pts_j = it_per_frame.point; tmp_feature.observation.push_back(make_pair(imu_j, Eigen::Vector2d{pts_j.x(), pts_j.y()})); } sfm_f.push_back(tmp_feature); } if (!relativePose(relative_R, relative_T, l)) { ROS_INFO("Not enough features or parallax; Move device around"); return false; } GlobalSFM sfm; if(!sfm.construct(frame_count + 1, Q, T, l, relative_R, relative_T, sfm_f, sfm_tracked_points)) // latest frame, { ROS_DEBUG("global SFM failed!"); marginalization_flag = MARGIN_OLD; return false; }- f_manager의 feature는 FeaturePerID의 리스트이다. 여기 들어있는 모든 feature에 대해 그 frame 번호와 point의 undistorted된 x,y를 pair로 만들어 sfm_f (SFMFeature의 vector)에 넣는다.
- sfm.construct를 통해 BA를 하는것에 실패하면 keyframe으로 지정하고 return false.
- bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l)
for (int i = 0; i < WINDOW_SIZE; i++) { vector<pair<Vector3d, Vector3d>> corres; corres = f_manager.getCorresponding(i, WINDOW_SIZE); if (corres.size() > 20) { double sum_parallax = 0; double average_parallax; for (int j = 0; j < int(corres.size()); j++) { Vector2d pts_0(corres[j].first(0), corres[j].first(1)); Vector2d pts_1(corres[j].second(0), corres[j].second(1)); double parallax = (pts_0 - pts_1).norm(); // 양 끝 frame의 차이를 계산하고 norm을 구함. sum_parallax = sum_parallax + parallax; } average_parallax = 1.0 * sum_parallax / int(corres.size()); if(average_parallax * 460 > 30 && m_estimator.solveRelativeRT(corres, relative_R, relative_T)) { l = i; ROS_DEBUG("average_parallax %f choose l %d and newest frame to triangulate the whole structure", average_parallax * 460, l); return true; } } }- getCorresponding 함수에서 start_frame ≤ i, WINDOW_SIZE ≤ end_frame을 만족하는 양끝의 point들을 가져온다. 따라서 i번째 corres에는 i와 WINDOW_SIZE 를 각 끝 frame으로 갖는 point가 들어 있다. 만약 20개 넘게 있다면, 이 양끝 point간의 parallax의 norm을 구한다. 이것들의 평균 * 460 > 30 이고 relative R,T를 구했다면, true를 반환한다.
- 또한 이 조건을 만족하는 i을 찾으면 l로 지정하고 return한다.
- bool MotionEstimator::solveRelativeRT(const vector<pair<Vector3d, Vector3d» &corres, Matrix3d &Rotation, Vector3d &Translation)
vector<cv::Point2f> ll, rr; for (int i = 0; i < int(corres.size()); i++) { ll.push_back(cv::Point2f(corres[i].first(0), corres[i].first(1))); rr.push_back(cv::Point2f(corres[i].second(0), corres[i].second(1))); } cv::Mat mask; // RANSAC을 이용해 fundamental matrix get (8-points algorithm도 가능) cv::Mat E = cv::findFundamentalMat(ll, rr, cv::FM_RANSAC, 0.3 / 460, 0.99, mask); cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1); cv::Mat rot, trans; int inlier_cnt = cv::recoverPose(E, ll, rr, cameraMatrix, rot, trans, mask); //cout << "inlier_cnt " << inlier_cnt << endl; // ll coordinate system to rr coordinate system Eigen::Matrix3d R; Eigen::Vector3d T; for (int i = 0; i < 3; i++) { T(i) = trans.at<double>(i, 0); for (int j = 0; j < 3; j++) R(i, j) = rot.at<double>(i, j); } Rotation = R.transpose(); Translation = -R.transpose() * T; if(inlier_cnt > 12) return true; else return false;- ll, rr에 corres에서 저장한 양끝 point들을 각각 저장한다. 이후 cv::findFundamentalMat에서 RANSAC을 이용해 ll과 rr간의 fundamental matrix를 찾는다. (ll , rr은 각각 한 frame안에서만 찾은 point들을 갖고 있으므로 가능하다.) 이때 five-point algorithm이 사용된다.
- 이미 normalize/undistorted 된 점들이므로 camera matrix는 I로 설정하고, fundamental matrix로 cv::recoverPose함수를 통해 ll → rr 로의 점변환 rot, trans matrix를 얻는다.
- 이를 Rotation(relative_R), Translation(relative_T)에 rr → ll 점변환 transformation matrix로 저장한다.
- bool GlobalSFM::construct(int frame_num, Quaterniond* q, Vector3d* T, int l,const Matrix3d relative_R, const Vector3d relative_T, vector
&sfm_f, map<int, Vector3d> &sfm_tracked_points) ... Pose[l].block<3, 3>(0, 0) = c_Rotation[l]; Pose[l].block<3, 1>(0, 3) = c_Translation[l]; ... Pose[frame_num - 1].block<3, 3>(0, 0) = c_Rotation[frame_num - 1]; Pose[frame_num - 1].block<3, 1>(0, 3) = c_Translation[frame_num - 1]; ... for (int i = l; i < frame_num - 1 ; i++) { // solve pnp if (i > l) { Matrix3d R_initial = c_Rotation[i - 1]; Vector3d P_initial = c_Translation[i - 1]; // R_initial, P_initial은 model -> camera system 점변환 if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f)) return false; c_Rotation[i] = R_initial; c_Translation[i] = P_initial; c_Quat[i] = c_Rotation[i]; Pose[i].block<3, 3>(0, 0) = c_Rotation[i]; Pose[i].block<3, 1>(0, 3) = c_Translation[i]; } // triangulate point based on the solve pnp result triangulateTwoFrames(i, Pose[i], frame_num - 1, Pose[frame_num - 1], sfm_f); } //3: triangulate l-----l+1 l+2 ... frame_num -2 for (int i = l + 1; i < frame_num - 1; i++) triangulateTwoFrames(l, Pose[l], i, Pose[i], sfm_f); //4: solve pnp l-1; triangulate l-1 ----- l // l-2 l-2 ----- l for (int i = l - 1; i >= 0; i--) { //solve pnp Matrix3d R_initial = c_Rotation[i + 1]; Vector3d P_initial = c_Translation[i + 1]; if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f)) return false; c_Rotation[i] = R_initial; c_Translation[i] = P_initial; c_Quat[i] = c_Rotation[i]; Pose[i].block<3, 3>(0, 0) = c_Rotation[i]; Pose[i].block<3, 1>(0, 3) = c_Translation[i]; //triangulate triangulateTwoFrames(i, Pose[i], l, Pose[l], sfm_f); } //5: triangulate all other points for (int j = 0; j < feature_num; j++) { if (sfm_f[j].state == true) continue; if ((int)sfm_f[j].observation.size() >= 2) { Vector2d point0, point1; int frame_0 = sfm_f[j].observation[0].first; point0 = sfm_f[j].observation[0].second; int frame_1 = sfm_f[j].observation.back().first; point1 = sfm_f[j].observation.back().second; Vector3d point_3d; triangulatePoint(Pose[frame_0], Pose[frame_1], point0, point1, point_3d); sfm_f[j].state = true; sfm_f[j].position[0] = point_3d(0); sfm_f[j].position[1] = point_3d(1); sfm_f[j].position[2] = point_3d(2); } }-
Pose[l] 에는 identity matrix와 zero가 들어감으로써 reference로 지정된다.
Pose[r]은 relative_R, relative_T 값을 갖는 matrix의 inverse를 갖게 되고, 이는 l → r의 점변환에 해당된다. - 먼저 i=l 에서 triangulateTwoFrames 함수를 통해, sfm_f에 들어있는 feature의 frame들에 대해, triangulate를 진행한다.
- 이후 i>l의 경우, solveFrameByPnP에서 i-1 relative_R, relative_T를 initial로 하여 Projection matrix(R_initial, P_initial)을 구하고, 이를통해 triangulateTwoFrames로 i번째 frame에서의 feature들의 3d Point를 구한다.
-
SUMMARY :
(1) l번째 frame, r번째 frame간의 Pose변환을 통해서 triangulate로 이 두 frame이 가지고 있는 feature의 3D point를 구한다.
(2) 이제 반대로 이 3D points를 이용해서 i=l+1부터의 image points에 대해 Projection matrix를 구하고, 이 Projection matrix와 Pose[r]을 통해 다시 triangulate하여 이전에 구하지 못했던 feature들의 3D point를 구한다.
(3) 이제 Pose[l]과 Pose[i]를 (projection matrix) 사용하여 다시 구해지지 않은 3D points들을 구한다. 이전에는 i와 r frame이 points를 갖고 있어야 하므로 지금은 l과 i frame을 갖는 points들을 구하는 것이다.
(4) 이제 l-1 ~ 0 frame과 l frame의 Projection matrix를 위와 동일한 방식으로 구해서 triangulate해서 3D points들을 구한다.
(5) 이제 모든 남은 feature의 first와 last frame의 projection matrix를 가지고 triangulate해준다.
-
- void GlobalSFM::triangulateTwoFrames(int frame0, Eigen::Matrix<double, 3, 4> &Pose0,int frame1, Eigen::Matrix<double, 3, 4> &Pose1,vector
&sfm_f) for (int j = 0; j < feature_num; j++) { if (sfm_f[j].state == true) continue; bool has_0 = false, has_1 = false; Vector2d point0; Vector2d point1; for (int k = 0; k < (int)sfm_f[j].observation.size(); k++) { if (sfm_f[j].observation[k].first == frame0) { point0 = sfm_f[j].observation[k].second; has_0 = true; } if (sfm_f[j].observation[k].first == frame1) { point1 = sfm_f[j].observation[k].second; has_1 = true; } } if (has_0 && has_1) { Vector3d point_3d; triangulatePoint(Pose0, Pose1, point0, point1, point_3d); sfm_f[j].state = true; sfm_f[j].position[0] = point_3d(0); sfm_f[j].position[1] = point_3d(1); sfm_f[j].position[2] = point_3d(2); } }- sfm_f은 feature ID 순서대로 들어가있고, 그 feature의 observation에는 frame번호와 feature point가 pair로 저장되어 있다.
- 따라서 위 함수에서 하는 일은, j번째 feature에 대해 frame0(l)이 있는지 체크하고, frame1(r) 이 있는지 체크하여, triangularPoint 함수로 point3d를 구하는 것이다. 이때 Pose0, Pose1은 P[l]과 P[r]에 해당된다. 이 point3d를 sfm_f[j] 즉 j번째 feature의 position으로 저장하게 된다. i=l에서 이것이 가능한 이유는, \(P_1\)X = x에서 \(P_1\)이 scale factor를 제외했을때 Identity이므로 X가 x의 homogenenous coordinate가 되서 \(P_2\)가 r번째 image x’으로의 projection matrix가 되기 때문이다.
- Triangulation의 formula 코드의 유도과정은 다음과 같다.
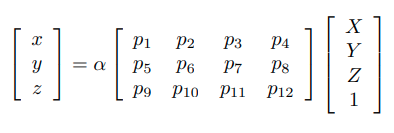
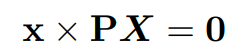
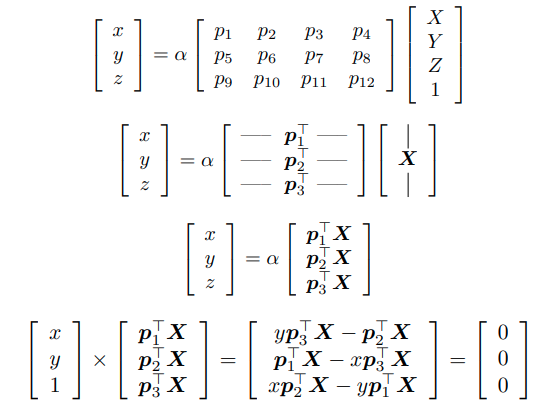
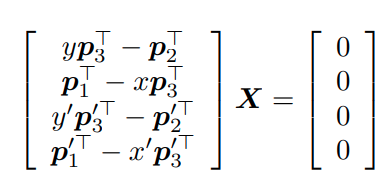
위와 같이 두 점으로부터 X와 관련된 식을 세울 수 있다. 이때 SVD를 이용하여,
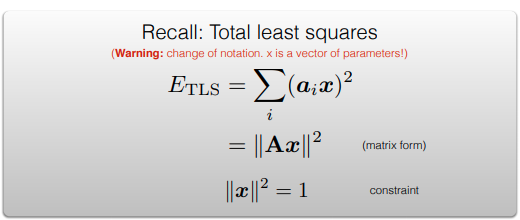
X를 구할 수 있고, point_3d는 code에서도 normalize된다.
[referenece] : http://www.cs.cmu.edu/~16385/s17/Slides/11.4_Triangulation.pdf
- bool GlobalSFM::solveFrameByPnP(Matrix3d &R_initial, Vector3d &P_initial, int i,vector
&sfm_f)
for (int j = 0; j < feature_num; j++) // 모든 feature 갯수만큼 (모든 frame에 다 고려)
{
if (sfm_f[j].state != true)
continue;
Vector2d point2d;
for (int k = 0; k < (int)sfm_f[j].observation.size(); k++) // 그 feature의 frame마다
{
if (sfm_f[j].observation[k].first == i)
{
Vector2d img_pts = sfm_f[j].observation[k].second;
cv::Point2f pts_2(img_pts(0), img_pts(1));
pts_2_vector.push_back(pts_2);
cv::Point3f pts_3(sfm_f[j].position[0], sfm_f[j].position[1], sfm_f[j].position[2]);
pts_3_vector.push_back(pts_3);
break;
}
}
}
...
pnp_succ = cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, 1);
...
cv::Rodrigues(rvec, r);
MatrixXd R_pnp;
cv::cv2eigen(r, R_pnp);
MatrixXd T_pnp;
cv::cv2eigen(t, T_pnp);
R_initial = R_pnp;
P_initial = T_pnp;
- 이제 cv::solvePnP 함수를 통해, 3D point에서 2D point로의 rvec, t 를 구한다. 이는 이때 iterative 방식(Levenberg-Marquardt optimization)을 사용하여 image point와 reprojected point간의 reprojection을 줄이는 optimization matrix를 얻는다. i-1 frame에서 얻은 것을 iteration의 initial로 사용한다.
- j번째 feature sfm_f에 i번째 frame이 있으면, pts_2_vector (normalized image point), pts_3_vector(point in 3D)에 각각 구한다. (이미 i=l에서 triangulation으로 sfm_f[j]의 position을 구한 것에 대해서만 진행한다.)
- 이제 projection matrix를 R_initial, P_initial로 반환한다.
2. Bundle Adjustment
1) bool GlobalSFM::construct(int frame_num, Quaterniond* q, Vector3d* T, int l,const Matrix3d relative_R, const Vector3d relative_T,vector
ceres::Problem problem;
ceres::LocalParameterization* local_parameterization = new ceres::QuaternionParameterization();
for (int i = 0; i < frame_num; i++)
{
...
problem.AddParameterBlock(c_rotation[i], 4, local_parameterization);
problem.AddParameterBlock(c_translation[i], 3);
if (i == l)
{
problem.SetParameterBlockConstant(c_rotation[i]);
}
if (i == l || i == frame_num - 1)
{
problem.SetParameterBlockConstant(c_translation[i]);
}
}
for (int i = 0; i < feature_num; i++)
{
if (sfm_f[i].state != true)
continue;
for (int j = 0; j < int(sfm_f[i].observation.size()); j++)
{
int l = sfm_f[i].observation[j].first;
ceres::CostFunction* cost_function = ReprojectionError3D::Create(
sfm_f[i].observation[j].second.x(),
sfm_f[i].observation[j].second.y());
problem.AddResidualBlock(cost_function, NULL, c_rotation[l], c_translation[l],
sfm_f[i].position);
}
}
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_SCHUR;
options.max_solver_time_in_seconds = 0.2;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
if (summary.termination_type == ceres::CONVERGENCE || summary.final_cost < 5e-03)
{
//cout << "vision only BA converge" << endl;
}
else
{
//cout << "vision only BA not converge " << endl;
return false;
}
for (int i = 0; i < frame_num; i++)
{
q[i].w() = c_rotation[i][0];
q[i].x() = c_rotation[i][1];
q[i].y() = c_rotation[i][2];
q[i].z() = c_rotation[i][3];
q[i] = q[i].inverse();
}
for (int i = 0; i < frame_num; i++)
{
T[i] = -1 * (q[i] * Vector3d(c_translation[i][0], c_translation[i][1], c_translation[i][2]));
}
for (int i = 0; i < (int)sfm_f.size(); i++)
{
if(sfm_f[i].state) // feature id를 key로하는 feature의 3D position을 value로 저장.
sfm_tracked_points[sfm_f[i].id] = Vector3d(sfm_f[i].position[0], sfm_f[i].position[1], sfm_f[i].position[2]);
}
return true;
- AddParameterBlock 함수를 통해 모든 frame의 Projection matrix들을 parameter로 추가함. local_parameterization는 manifold 연산을 위해 rotation에 대해 추가함.
- 단, l번째 frame의 rotation과 translation, 그리고 last frame(WINDOW_SIZE)의 translation은 기준으로 잡아야 하므로 SetParameterBlockConstant를통해 이 둘은 고정시킨다.
- 모든 feature의 각 frame에 대해 ReprojectionError3D structure를 통해 cost function을 정의하고, AddresidualBlock을 통해 parameter로 start frame의 projection matrix 값들 (c_rotation[], c_translation[])과 i번째 frame의 3D points를 지정한다.
- 이후 BA를 수행하여 parameter 값들을 얻는다. 이 값들을 T[i], q[i]에 각 frame에서의 transformation들의 inverse, 즉, i frame → ref(원래 l) frame으로의 점변환을 저장한다.
- sfm_tracked_points에는 각 feature id에 sfm_f에서 구해둔 3D points를 저장한다.
2) struct ReprojectionError3D의 operator()
bool operator()(const T* const camera_R, const T* const camera_T, const T* point, T* residuals) const
{
T p[3];
ceres::QuaternionRotatePoint(camera_R, point, p);
p[0] += camera_T[0]; p[1] += camera_T[1]; p[2] += camera_T[2];
T xp = p[0] / p[2];
T yp = p[1] / p[2];
residuals[0] = xp - T(observed_u);
residuals[1] = yp - T(observed_v);
return true;
}
- ceres가 residual을 계산하는 식을 적는 방식으로, ceres::QuaternionRotatePoint가 camera_R을 통해 3D point를 rotate시켜 p에 저장한다. 이후 translation하고 normalized 한 후 reprojection error를 비교한다.
3. Solve pnp for all frames
1) bool Estimator::initialStructure()
for (int i = 0; frame_it != all_image_frame.end( ); frame_it++)
{
// provide initial guess
cv::Mat r, rvec, t, D, tmp_r;
// 이미지 Frame의 time이 Header와 같은경우. Headers에는 각 frame에 대한 time이 들어있다.
// 즉, WINDOW내에 있는 frame인 경우 넘어감.
if((frame_it->first) == Headers[i])
{
frame_it->second.is_key_frame = true;
// icam to lcam * body to cam => body to lcam (점변환 기준)
// lcam이 initial이 되는 것.
frame_it->second.R = Q[i].toRotationMatrix() * RIC[0].transpose();
frame_it->second.T = T[i];
i++;
continue;
}
if((frame_it->first) > Headers[i])
{
i++;
}
// 나머지 경우 : frame의 시간이 header보다 작은 경우
// Window 내에 있지 않다는 의미이므로 pnp가 되지 않았을 것이라는 것.
// 그렇다면 이미 아는 feature들을 이용해서 pnp를 풀어줌.
Matrix3d R_inital = (Q[i].inverse()).toRotationMatrix();
Vector3d P_inital = - R_inital * T[i];
cv::eigen2cv(R_inital, tmp_r);
cv::Rodrigues(tmp_r, rvec);
cv::eigen2cv(P_inital, t);
frame_it->second.is_key_frame = false;
vector<cv::Point3f> pts_3_vector;
vector<cv::Point2f> pts_2_vector;
for (auto &id_pts : frame_it->second.points)
{
int feature_id = id_pts.first;
for (auto &i_p : id_pts.second)
{
it = sfm_tracked_points.find(feature_id);
if(it != sfm_tracked_points.end())
{
Vector3d world_pts = it->second;
cv::Point3f pts_3(world_pts(0), world_pts(1), world_pts(2));
pts_3_vector.push_back(pts_3);
Vector2d img_pts = i_p.second.head<2>();
cv::Point2f pts_2(img_pts(0), img_pts(1));
pts_2_vector.push_back(pts_2);
}
}
}
cv::Mat K = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
if(pts_3_vector.size() < 6)
{
cout << "pts_3_vector size " << pts_3_vector.size() << endl;
ROS_DEBUG("Not enough points for solve pnp !");
return false;
}
if (! cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, 1))
{
ROS_DEBUG("solve pnp fail!");
return false;
}
cv::Rodrigues(rvec, r);
MatrixXd R_pnp,tmp_R_pnp;
cv::cv2eigen(r, tmp_R_pnp);
R_pnp = tmp_R_pnp.transpose();
MatrixXd T_pnp;
cv::cv2eigen(t, T_pnp);
T_pnp = R_pnp * (-T_pnp);
frame_it->second.R = R_pnp * RIC[0].transpose();
frame_it->second.T = T_pnp;
}
- Headers[i]에는 i번째 frame의 time이 들어있다. all_image_frame에는 처음부터 순서대로 frame의 feature들이 들어있다.
- frame_it->first == Headers[i] 인 경우는 sliding window안에 있는 frame에 대한 작업이다. all_frame_image의 해당 frame을 key frame으로 등록하고, (i camera frame → l camera frame) * (IMU to i camera frame) = (i frame에서의 IMU to reference frame) 의 rotation matrix와 i camera to reference frame의 translation을 점변환으로 저장한다.
-
Headers[i]와 frame_it -> first가 동일하지 않다면, initialStructure를 성공하기 전에 있던 Window내에 없는 frame(relativePose나 sfm.construct 실패로 인해 Window 이전의 frame이 되거나(i=0))이나 non-keyframe이 image로 들어올때 sliding으로 인해 Headers의 마지막 부분만 바뀌어 time들이 불연속적으로 되는 현상 때문이다.
(frame_it -> first가 Headers[i]보다 큰 경우는 아직 보지 못함)
이 경우 initial 값을 가장 가까운 i를 사용하여 sfm_tracked_points에서 해당 frame의 feature를 찾으면, solve PnP 한다. (key frame에서는 제외한다.) 또한 마찬가지로 all_image_frame에 들어 있는 frame_it의 R,T 값을 지정해준다.
4. Visual Initial Alignment
1) bool Estimator::visualInitialAlign()
...
bool result = VisualIMUAlignment(all_image_frame, Bgs, g, x);
...
// change state
for (int i = 0; i <= frame_count; i++)
{
Matrix3d Ri = all_image_frame[Headers[i]].R;
Vector3d Pi = all_image_frame[Headers[i]].T;
Ps[i] = Pi;
Rs[i] = Ri;
all_image_frame[Headers[i]].is_key_frame = true;
}
double s = (x.tail<1>())(0);
for (int i = 0; i <= WINDOW_SIZE; i++)
{
pre_integrations[i]->repropagate(Vector3d::Zero(), Bgs[i]);
}
for (int i = frame_count; i >= 0; i--)
Ps[i] = s * Ps[i] - Rs[i] * TIC[0] - (s * Ps[0] - Rs[0] * TIC[0]);
int kv = -1;
map<double, ImageFrame>::iterator frame_i;
for (frame_i = all_image_frame.begin(); frame_i != all_image_frame.end(); frame_i++)
{
if(frame_i->second.is_key_frame)
{
kv++;
Vs[kv] = frame_i->second.R * x.segment<3>(kv * 3);
}
}
Matrix3d R0 = Utility::g2R(g);
double yaw = Utility::R2ypr(R0 * Rs[0]).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
g = R0 * g;
//Matrix3d rot_diff = R0 * Rs[0].transpose();
Matrix3d rot_diff = R0;
for (int i = 0; i <= frame_count; i++)
{
Ps[i] = rot_diff * Ps[i];
Rs[i] = rot_diff * Rs[i];
Vs[i] = rot_diff * Vs[i];
}
ROS_DEBUG_STREAM("g0 " << g.transpose());
ROS_DEBUG_STREAM("my R0 " << Utility::R2ypr(Rs[0]).transpose());
f_manager.clearDepth();
f_manager.triangulate(frame_count, Ps, Rs, tic, ric);
- VisualIMUAlignment 함수에서 solveGyroscopeBias, LinearAlignment함수를 호출한다.
- Rs, Ps에 각각 (i frame에서의 IMU to reference frame) 의 rotation, i camera to reference frame의 translation을 의미하는 값을 가져온다. 즉 \(q^{c_0}_{b_k}\), \(p_{c_k}^{c_0}\) 이다. 이것들을 사용해 마찬가지로 pre_integrations도 repropagate해주고, 다음식을 사용해 IMU frame에서의 Ps(\(**p_{b_k}^{c_0}**\)) 를 구한다.
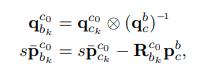
또한 Vs(\(**v_{b_k}^{c_0}**\)) 도 \(q_{b_k}^{c_0}\)를 이용해 구해준다.
-
g2R에서 (0,0,1) 즉 world frame의 gravity와의 차이에 해당하는 R0를 구한 것이므로 R0 = \(q_{c_0}^w\)가 된다. 그런데 이제 R0 와 \(q_{b_0}^{c_0}\)를 곱하여 얻어진 \(q_{b_0}^w\)에서도 yaw값이 정해지지 않았으므로, 이 yaw값을 빼주어야 진정한 world frame으로의 변환을 갖게된다.(c0의 영향을 최소화 및 삭제한다고 생각하면 된다.
이제, 이 body frame에서 yaw값이 지워진 R0 = \(q_{c_0}^w\)을 사용하여 world frame으로 Ps, Rs, Vs를 바꿔준다. 또한 gravity vector역시 world frame으로 변환한다. (\(g^{c_0}\) → \(g^{w}\))
-
마지막으로 f_manger.triangulate 함수를 통해 metric unit으로 depth를 재설정한다.
2) void solveGyroscopeBias(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs)
...
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(3, 3);
VectorXd tmp_b(3);
Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
A += tmp_A.transpose() * tmp_A;
b += tmp_A.transpose() * tmp_b;
}
delta_bg = A.ldlt().solve(b);
for (int i = 0; i <= WINDOW_SIZE; i++)
Bgs[i] += delta_bg;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
{
frame_j = next(frame_i);
frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
}
- frame_i의 R과 T는 각각 (i frame에서의 IMU to reference frame) 의 rotation, i camera to reference frame의 translation를 나타낸다.
- 코드의 q_ij는 \(q_{b_{k+1}}^{c_{0}}{}^{-1}\)\(q_{b_k}^{c_0}\)을 나타낸다. 아래의 식을 생각해보면, delta_q.inverse()는 \(\hat\gamma_{b_{k+1}}^{b_k}{}^{-1}\)가 된다. 또한 아래식을 최소화하는 min을 구하므로, \(q_{b_{k+1}}^{c_{0}}{}^{-1}\) \(q_{b_k}^{c_0}\) - \(\gamma_{b_{k+1}}^{b_k}{}^{-1}\) = 0을 만족하는 \(\delta b_g\)를 구하는 것이 된다. (코드는 VINS-Mobile의 식과 결합하여 red box 부분을 사용하였다.)
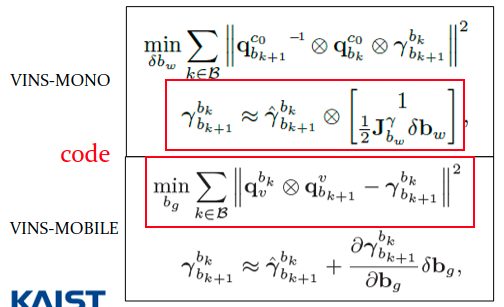
(위 두 사진은 KAIST Urban Robotics Lab의 임현준 박사과정님이 발표하신 자료에서 발췌하였습니다.)
-
따라서 위의 식을 \(\delta b_g\)에 대해 정리하면,
\(\frac{\delta \gamma}{\delta b_g} * \delta b_g\) = 2 * \(\gamma_{b_{k+1}}^{b_k}{}^{-1}\) * \(q^{b_k}_{b_{k+1}}\)
이 되고, 코드는 위 식을 Cholesky decomposition을 통해 해를 구하는 것이 된다.
- 그런데 각 frame에 대해 \(\delta b_g\)를 구할 수 있으나, 전부다 더하여 한번에 구하는 것으로 보인다. (Cholesky decomposition이 load가 커서..?)
- 이후 모든 frame에 대해 Bgs[i]에 전부 넣어주어서 initialize해주고, repropagate해서 jacobian등을 다시구하게 된다.
3) bool LinearAlignment(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
int n_state = all_frame_count * 3 + 3 + 1; // count * (x, y, z) + gravity * (x, y, z) + scale
MatrixXd A{n_state, n_state};
VectorXd b{n_state};
map<double, ImageFrame>::iterator frame_i;
map<double, ImageFrame>::iterator frame_j;
int i = 0;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(6, 10);
VectorXd tmp_b(6);
double dt = frame_j->second.pre_integration->sum_dt;
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
//cout << "delta_p " << frame_j->second.pre_integration->delta_p.transpose() << endl;
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;
//cout << "delta_v " << frame_j->second.pre_integration->delta_v.transpose() << endl;
Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
b.tail<4>() += r_b.tail<4>();
A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
}
A = A * 1000.0;
b = b * 1000.0;
x = A.ldlt().solve(b);
double s = x(n_state - 1) / 100.0;
ROS_DEBUG("estimated scale: %f", s);
g = x.segment<3>(n_state - 4);
ROS_DEBUG_STREAM(" result g " << g.norm() << " " << g.transpose());
if(fabs(g.norm() - G.norm()) > 0.5 || s < 0)
{
return false;
}
RefineGravity(all_image_frame, g, x);
s = (x.tail<1>())(0) / 100.0;
(x.tail<1>())(0) = s;
if(s < 0.0 )
return false;
else
return true;
- camera center에서 IMU로 바꾸는 extrinsic parameter \(p_c^b, q_c^b\) 를 사용하여, 다음과 같이 pose를 IMU center로 변환할 수 있다.
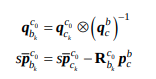
- 또한 world frame을 \(c_0\) frame으로 정하면, 5번식의 pre-integration을 위식을 이용하여
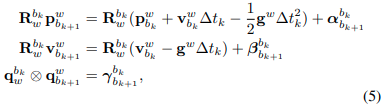
다음과 같이 정리할 수 있다.
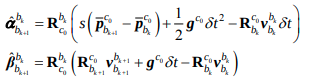
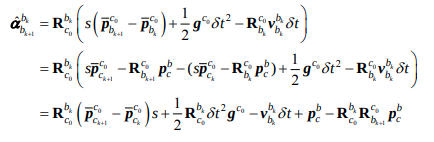
코드는 아래 식을 tmp_b = tmp_A * x로 표현한 것이고
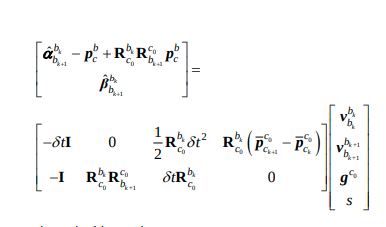
이는 논문에서 아래식에서 유도된 것이다.
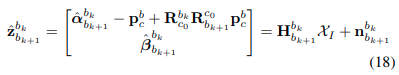
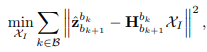
결국 x는 다음식과 같은 모든 frame에 대한 state를 구하게 된다.
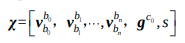
이는 모든 frame에서 body frame에 대한 velocity와 reference frame에 대한 gravity, scale parameter를 의미한다.
- 코드상에서 large A로 합쳐서 Cholesky decomposition을 사용하는데, 이때 <3, 3> block씩 겹치는 이유는 tmp_A와 tmp_b로 구하는 x가 k frame과 k+1 frame에 대해서 구하는 것이고, tmp_A.transpose * tmp_A 행렬에서 정사각행렬을 만들어 g, s부분을 제외한 k, k+1 frame에 관한 parameter를 쭉 이어서 더해주므로, k - k+1 / k+1 - k+2 /… 처럼 <3, 3> 씩 겹치게 되어서 더해주게 되는 것이다.
- 이후 RefineGravity함수로 Gravity Refinement가 수행된다.
4) void RefineGravity(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
Vector3d g0 = g.normalized() * G.norm();
Vector3d lx, ly;
int all_frame_count = all_image_frame.size();
int n_state = all_frame_count * 3 + 2 + 1; // (x,y,z) * count + w1, w2, g scale
MatrixXd A{n_state, n_state};
VectorXd b{n_state};
...
for(int k = 0; k < 4; k++)
{
MatrixXd lxly(3, 2);
lxly = TangentBasis(g0);
int i = 0;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(6, 9);
VectorXd tmp_b(6);
double dt = frame_j->second.pre_integration->sum_dt;
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
tmp_A.block<3, 2>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity() * lxly;
tmp_A.block<3, 1>(0, 8) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0] - frame_i->second.R.transpose() * dt * dt / 2 * g0;
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
tmp_A.block<3, 2>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity() * lxly;
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v - frame_i->second.R.transpose() * dt * Matrix3d::Identity() * g0;
Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<3, 3>() += r_A.bottomRightCorner<3, 3>();
b.tail<3>() += r_b.tail<3>();
A.block<6, 3>(i * 3, n_state - 3) += r_A.topRightCorner<6, 3>();
A.block<3, 6>(n_state - 3, i * 3) += r_A.bottomLeftCorner<3, 6>();
}
A = A * 1000.0;
b = b * 1000.0;
x = A.ldlt().solve(b);
VectorXd dg = x.segment<2>(n_state - 3);
g0 = (g0 + lxly * dg).normalized() * G.norm();
//double s = x(n_state - 1);
}
g = g0;
- g0는 이전 gravity vector의 nomalized 방향 * G (0,0,9.8) 이다.
- TargnetBasis함수에서, g0에 수직인 두 vector를 얻게 된다. 코드에서는 다음 식
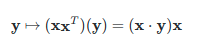
을 사용하여, a에 orthogonal한 basis b를 얻는다.
- 이제 이전의 LinearAlignment 식에서 gravity부분을 다음식으로 대체하여 다시 state를 구하여 대체한다. (4번으로 converge한다고 추정하는 듯 하다.)
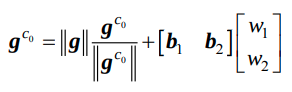
5) void FeatureManager::triangulate(int frameCnt, Vector3d Ps[], Matrix3d Rs[], Vector3d tic[], Matrix3d ric[])
for (auto &it_per_id : feature)
{
if(it_per_id.feature_per_frame.size() > 1)
{
int imu_i = it_per_id.start_frame;
Eigen::Matrix<double, 3, 4> leftPose;
Eigen::Vector3d t0 = Ps[imu_i] + Rs[imu_i] * tic[0];
Eigen::Matrix3d R0 = Rs[imu_i] * ric[0];
leftPose.leftCols<3>() = R0.transpose();
leftPose.rightCols<1>() = -R0.transpose() * t0;
imu_i++;
Eigen::Matrix<double, 3, 4> rightPose;
Eigen::Vector3d t1 = Ps[imu_i] + Rs[imu_i] * tic[0];
Eigen::Matrix3d R1 = Rs[imu_i] * ric[0];
rightPose.leftCols<3>() = R1.transpose();
rightPose.rightCols<1>() = -R1.transpose() * t1;
Eigen::Vector2d point0, point1;
Eigen::Vector3d point3d;
point0 = it_per_id.feature_per_frame[0].point.head(2);
point1 = it_per_id.feature_per_frame[1].point.head(2);
triangulatePoint(leftPose, rightPose, point0, point1, point3d);
Eigen::Vector3d localPoint;
localPoint = leftPose.leftCols<3>() * point3d + leftPose.rightCols<1>();
double depth = localPoint.z();
if (depth > 0)
it_per_id.estimated_depth = depth;
else
it_per_id.estimated_depth = INIT_DEPTH;
continue;
}
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (it_per_id.used_num < 4)
continue;
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;
Eigen::MatrixXd svd_A(2 * it_per_id.feature_per_frame.size(), 4);
int svd_idx = 0;
Eigen::Matrix<double, 3, 4> P0;
Eigen::Vector3d t0 = Ps[imu_i] + Rs[imu_i] * tic[0];
Eigen::Matrix3d R0 = Rs[imu_i] * ric[0];
P0.leftCols<3>() = Eigen::Matrix3d::Identity();
P0.rightCols<1>() = Eigen::Vector3d::Zero();
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
Eigen::Vector3d t1 = Ps[imu_j] + Rs[imu_j] * tic[0];
Eigen::Matrix3d R1 = Rs[imu_j] * ric[0];
Eigen::Vector3d t = R0.transpose() * (t1 - t0);
Eigen::Matrix3d R = R0.transpose() * R1;
Eigen::Matrix<double, 3, 4> P;
P.leftCols<3>() = R.transpose();
P.rightCols<1>() = -R.transpose() * t;
Eigen::Vector3d f = it_per_frame.point.normalized();
svd_A.row(svd_idx++) = f[0] * P.row(2) - f[2] * P.row(0);
svd_A.row(svd_idx++) = f[1] * P.row(2) - f[2] * P.row(1);
if (imu_i == imu_j)
continue;
}
ROS_ASSERT(svd_idx == svd_A.rows());
Eigen::Vector4d svd_V = Eigen::JacobiSVD<Eigen::MatrixXd>(svd_A, Eigen::ComputeThinV).matrixV().rightCols<1>();
double svd_method = svd_V[2] / svd_V[3];
it_per_id.estimated_depth = svd_method;
if (it_per_id.estimated_depth < 0.1)
{
it_per_id.estimated_depth = INIT_DEPTH;
}
}
-
첫 if문에서 Rs, Ps ( \(q^{w}_{b_k}\), \(p_{b_k}^{w}\) )에 tic[0], ric[0] 등을 곱함으로써,
t0는 world frame에서 camera의 위치(Translation : camera k to world frame)
R0는 camera k to world frame rotation 변환이 된다.
이후 leftPose는 이들의 역변환을 넣어줌으로써, world frame to camera frame k transformation matrix가 된다.
(마찬가지로 rightPose는 다음 k+1 frame에 대한 변환이 된다.)
이제 triangulatePoint함수를 이용해 world frame에서의 point3d를 구할 수 있고, 이를 camera frame으로 변환하여 해당 feature의 depth를 구할 수 있다. -
만약, feature가 들어 있는 다른 모든 frame의 정보도 활용하기 위해, SVD와 triangulation 수식을 혼합하여 estimated_depth를 구한다. (현재는 미사용)
VINS-Fusion 코드를 정리한 포스트입니다.
- VINS-Fusion Code Review - (1) Image Processing
- VINS-Fusion Code Review - (2) IMU Processing
- VINS-Fusion Code Review - (3) Initialization
- VINS-Fusion Code Review - (4) Sliding window & Optimization
- VINS-Fusion Code Review - (5) Marginalization
- VINS-Fusion Code Review - (6) Graph optimization
Reference
- [2017] Quaternion kinematics for the error-state Kalman filter.pdf
- [2005] Indirect Kalman Filter for 3D Attitude Estimation.pdf
- Formula Derivation and Analysis of the VINS-Mono.pdf
- Marginalization&Shcurcomplement.pptx
- [TRO2012] Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions.pdf
- VINS-Mono.pdf